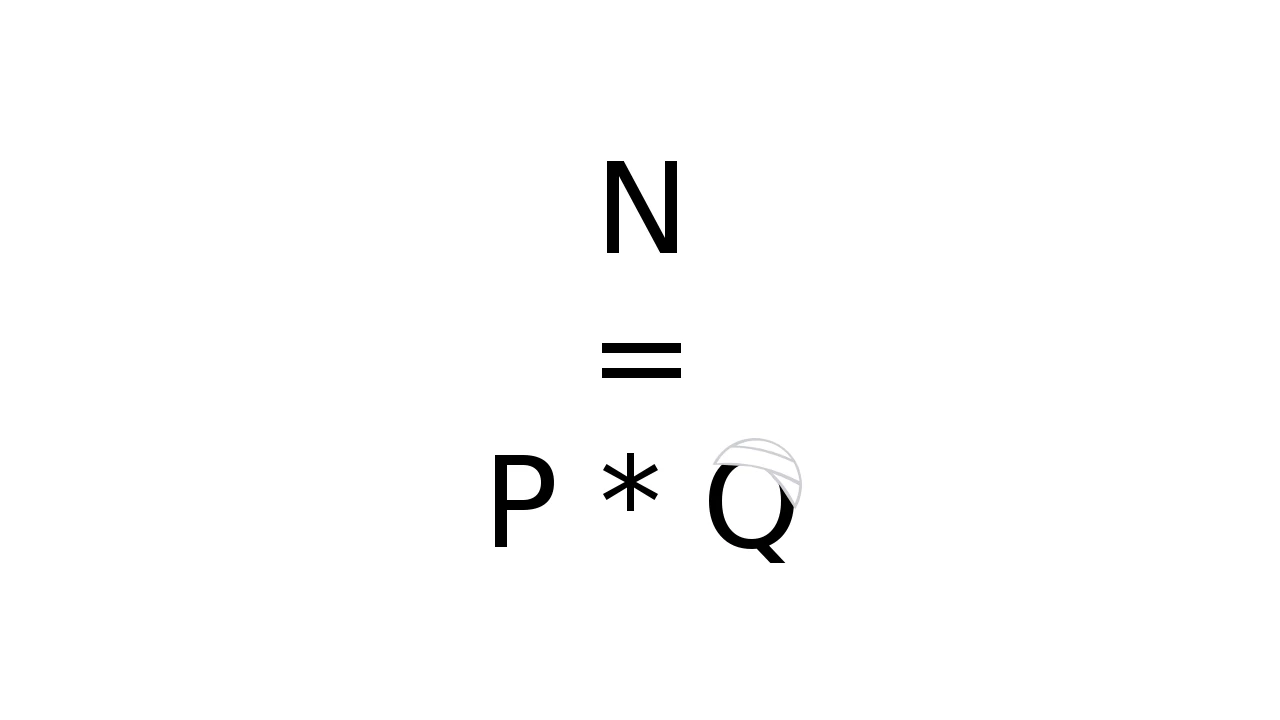
Backdooring RSA
You have probably heard about backdoors in different software, the dlink user-agent backdoor[1] is a classic. These backdoors typically allow attackers to bypass the standard authorization and gain access to a system. While this is bad, it is arguably quite easy to spot, especially if the source code is provided. However, it becomes more challenging when the attackers masquerade the backdoors as bugs, for example by intentionally including a buffer overflow in the code. A similar example is an old WhatsApp bug[2] that could have been a potential backdoor. As bad as this sounds, it comes nowhere near to the horror of cryptographic backdoors.
The main idea behind cryptographic backdoors is that an attacker should be able to recover plain texts from ciphertexts or private keys from public keys. I recommend this great article[3] about cryptographic backdoors if you are interested. The researchers showed that they could create an encryption algorithm, BEA-1, that passed all cryptographic tests, even though it contained a backdoor.
What I want to do in this post is to try to see if a robust and safe cryptographic algorithm like RSA can be slightly modified in order to introduce a backdoor. More formally, I want to create a generator G' that takes the size of the modulus N as input and outputs p and q, and the following must hold:
- Given N, an attacker should quickly be able to recover p and q from the private key.
- A victim should not be able to easily identify if N was generated by G'.
- A victim should not be able to easily identify if p and q were generated by G'.
Let's do some examples! The table below contains 5 180-bit RSA moduli, which should take about 10 seconds each to crack, can you guess which one is backdoored?
| 1 | 2285391608451469299206740632596490630247594198779663721 |
| 2 | 2154587883944544623774933436201285307697796347162878297 |
| 3 | 2983956810648093240792265689077797628407464901309281109 |
| 4 | 2714281865503470320865169352512043791852563130460572123 |
| 5 | 2954078889729608335241458876608461702484203246302252627 |
Well, of course, this is not really possible without knowing the backdooring algorithm, I could just have said my backdoor is "always use some specific p". Now as Kerckhoffs would have said, we should not rely on our algorithm to be confidential, so here is the mathematica file and pseudocode:
Pick a secret base b and resolution r.
Generate p and q as you normally would.
Calculate x as Ceil[Log[b,q]*r]
Calculate q' as NextPrime[b^(x/r)]
N = p * q'
return (p, q', N)
To find the private key based on N, all the attacker have to do is try all possible values of x, generate q' and see if q' divides N. Notice that the algorithm is designed such that x will grow linearly with size (number of bits) of N. Going back to the examples above. Even if you know the algorithm you still need to know b and r in order to quickly brute force x, making the backdoor hard to detect solely by inspection of N. For the example above, b was 7 and r was 10. In its essence, this algorithm is a pseudo-random (prime) number generator, seeded by b and r, that returns a linear amount of numbers for a given size of N. The limiting factor in the algorithm above is that r will limit the number of possible values for q, meaning that if you have more than r keys then you could spot this backdoor. Still, since cracking takes linear time, r could be quite large and yet allow for fast cracking.
Well, how can this be used? This method can be useful if an attacker can gain access to a cryptographic key generator and inject this backdoor. Remember, the attacker will not need to save the keys or try to exfiltrate them. This type of attack could, for example, be viable in a supply chain attack. It could also be useful in a system where you don't want the users to be able to read others traffic, but still have an administrator that could read all the traffic. In this case, the administrator could use b and r as a master key to acquire p and q.
Notes
- http://www.devttys0.com/2013/10/reverse-engineering-a-d-link-backdoor/
- https://tobi.rocks/2016/04/whats-app-retransmission-vulnerability/
- https://www.theregister.co.uk/2017/12/15/crypto_mathematical_backdoors/
Write your comment!
Comments
PrevPrime(q_i') < (b^(1/r))^x <= q_i'
If all ranges are excluded, this algorithm is not being used.
Otherwise, calculating gcd of about sqrt(xmax) pairs of N has a good chance of yielding at least one common factor because of the birthday paradox... :)